GRAPH THEORY PART II

UNDIRECTED GRAPHS

Definition 01:graph
A graph G is an ordered pair of elements, G = where V(G) is a non-empty finite set of elements, called vertices (singular is vertex) and E(G) is a set of unordered pairs of elements called edges and are denoted by [x,y], x,y Є V(G).

Definition 02:DEGREE OF VERTEX X

The degree of a vertex x in a graph G denoted by deg(x) is the number of edges incident to x where a loop is counted twice.

Definition 03:ISOLATED VERTEX
A vertex x is an isolated vertex if deg(x) = 0

Definition 04:SIMPLE GRAPH
Simple graph is a graph with no loops and no multiple edges.

Definition 05:ORDER AND SIZE

Let G be a graph, the order of G is │V(G)│ while the size of G is │E(G)│.

Definition 06:R-REGULAR

A graph G is said to be r-regular if deg(x) = r for all x Є V(G).

Definition 07:WALK
Let G be a graph, a walk of length K is a sequence [x₁, x₂, .. x_k, x_k+1], x₁, x₂, .. x_k+1 Є V(G) such that [x_i, x_i+1] Є E(G) for all 1 ≤ i ≤ k.

Definition 08:CLOSED WALK
A walk is said to be closed if x₁ = x_k+1 and k > 0.

Definition 09:PATH
A walk is called a path if the terms of the sequence are distinct.

Definition 10:CYCLE
A walk is called a cycle, if it is closed, its edges are distinct and if [x_1, x_2, x_{3, …} x_k] are distinct. A cycle is denoted by C_n where n is the number of vertices.

Definition 11:DISTANCE
The distance between vertices u and v, denoted by d(u,v), is the length of the shortest path connecting u to v. If no paths between u and v exists, then d(u,v) is not defined.

Definition 12:CONNECTED GRAPH AND DISCONNECTED GRAPH
A graph G is connected if there is a path between x and y for all x,y Є V(G). A graph which is not connected is said to be disconnected.

Definition 13:DIAMETER
The diameter of a connected graph G denoted by d(G) is the maximum distance between its two vertices.

Definition 14:SUBGRAPH
Let G be a graph, we call H a subgraph of G if V(H) is a subset of V(G) and E(H) is a subset of E(G).

Definition 15:SPANNING SUBGRAPH

If H is a subgraph of G and V(H) = V(G) then H is a spanning subgraph of G.

Definition 16:PROPER SUBGRAPH

Let G and H be graphs. If H is a subgraph of G but H ≠ G, then H is a proper subgraph of G.

Definition 17:COMPONENT

A connected component of G (or simply component) is any maximal connected subgraph of G.

Definition 18:COMPLEMENT

Let G be a graph. The complement of G_, denoted by Ğ is the simple graph with V(G) = V(Ğ) and for all [x,y] Є E(Ğ) iff [x,y] is not an element of E(G).

Definition 19:ISOMORPHISM

Let H and G be graphs. A mapping Ø : V(G) -> V(H) is called isomorphism if Ø is bijective and [x,y] Є E(G) iff [Ø(x), Ø(y)] Є E(H). We say that G is isomorphic to H if there exist an isomorphism Ø : V(G) -> V(H).

Definition 20:SELF-COMPLEMENTARY

A graph is called a self complementary if G ~ Ğ.

Definition 21:ACYCLIC

A graph which does not contain cycles is called acyclic.

Definition 22:TREE

A connected acyclic graph is called a tree.

Definition 23:END VERTEX / PENDANT / LEAF

A vertex x in a tree is called an end vertex / pendant vertex / leaf if degree x = 1.

Definition 24:FOREST

A forest is a graph with the property

Definition 25:CUT VERTEX

A vertex x is called a cut vertex if the removal of x increases the number of components in G.

Definition 26:BRIDGE

A bridge is an edge whose removal increases the number of components of a graph.

Definition 27:BLOCK

A block is a graph with no cut vertex

Definition 28:COMPLETE GRAPH

A complete graph denoted by K_n where n is the order of K_n, is a simple graph such that [x,y] Є E(Kn) for all x,y Є V(Kn) and x ≠ y.

Definition 29:BIPARTITE GRAPH

A graph G is bipartite if V(G) can be partitioned into two subsets x and y such that each edge joins a vertex in x to a vertex in y. A bipartite graph with m vertices in x and n vertices in y is denoted by B_mn.

Definition 30:COMPLETE BIPARTITE GRAPH

A graph G is a complete bipartite if V(G) can be partitioned into two subsets x and y such that every vertex in x is joined in every vertex in y. It is denoted by K_mn.

Definition 31:PLANAR GRAPH

A graph G is called a planar graph if it is possible to draw G in the plane without edge crossing.

Definition 32:STAR

A star is a graph denoted by S_n if there are n-1 end vertices incident to a vertex x called the central vertex.

Definition 33:HAMILTONIAN GRAPH

A graph G is said to be Hamiltonian if it contained a spanning cycle.

Definition 34:EULERIAN GRAPH

A graph G is said to be Eulerian if it is a closed, spanning walk using each edge of G only-once / exactly-once.

Definition 35:CARTESIAN PRODUCT

Let G and H be two graphs. The Cartesian Product of G and H which is denoted by G x H is the graph with V(GxH) = V(G) x V(H) and ordered pairs (x,y) and (u,v) are adjacent if and only if x = u and [y,v] Є E(H) or y = v and [x,u] Є E(G).

Definition 36:SUM OF G AND H

Let G and H be two graphs with disjoint vertex sets. The sum of G and H denoted by G+H is the graph with V(G+H) = V(G) U V(H) and E(G+H) = E(G) U E(H) U { [x,y] such that x Є V(G), y Є V(H) }.

Definition 37:VERTEX GLUING

Let G and H be two graphs with disjoint vertex sets. A vertex gluing of G and H denoted by G*H is a union of a vertex x in V(G) and a vertex y in V(H) where E(G*H) = E(G) U E(H).

Definition 38:INDEPENDENT SET

Let G be a graph, a set S of V(G) is called an independent set if for all x,y Є S, [x,y] is not an element of E(G).

Definition 39:LABELLING F

A labelling f of a graph G is a one to one function f : V → Z⁺.

Definition 40:GRACEFULL LABELLING

Let G be a graph with m edges. A graceful labelling of G is a one to one mapping f : V(G) → { 0, 1, 2, 3, …m } such that the induced mapping f* : E(G) → { 1, 2, 3, …m } is defined by f* (U_i , U_i+1) = │f (U_i+1) – f (U_i)│is one to one function and onto function.

Definition 41:GRACEFUL

A graph which admits a graceful labelling is said to be graceful.

Definition 42:CROWN

A crown denoted by Cr_n is a cycle with a pendant edge attached at each vertex. (n denotes the order of the cycle)

Definition 43:FLOWERETTE

Let x and y be any two cycle vertices adjacent to a cycle vertex z of a crown which cycle C_n and v be the pendant vertex adjacent to z. A flowerette, denoted by Ft_n is a graph obtained by deleting the pendant edge attached to z, joining the pendant vertex v to each x and y and then repeating the procedures using all the other pendant edges and vertices.

DIRECTED GRAPHS

Definition 44:digraph
A digraph (or directed graph) D is a finite set V of objects called vertices together with a set A of ordered pairs of distinct vertices. The elements of A are called directed edges or arcs.

D₁:

Definition 45ORIENTED GRAPH
If a digraph D has the property that for each pair u,v of distinct vertices of D, at most one of (u,v) and (v,u) is an arc of D, then D is an oriented graph.

D₁:

Definition 46:ADJACENT TO AND ADJACENT FROM
If (u,v) Є A(D), then u is said to be adjacent to v and v is adjacent from u.

D₁:

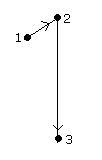Vertex 1 is adjacent to vertex 2.

Vertex 2 is adjacent to vertex 3.

Vertex 3 is adjacent from vertex 2.

Vertex 2 is adjacent from vertex 1.

Definition 47:OUT DEGREE AND IN DEGREE
The number of vertices to which a vertex u is adjacent, is the out degree of v, and is denoted by od(v). On the other hand, the number of vertices from which a vertex u is adjacent, is the in degree of v, and is denoted by id(v)

D₁:

od(1): 1 id(1): 0

od(2): 1 id(2): 1

od(3): 0 id(3): 1

Definition 48:SOURCE
A vertex v in V(D) is a source if:
od(v) > 1
id(v) = 0

D₁:

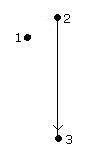
Sources in D₁ is vertex 1.

Definition 49:SINK
A vertex v in V(D) is a sink if:
od(v) = 0
id(v) > 1

D₁:

Sink in D₁ is vertex 3.

Definition 50:CARRIER
A vertex v in V(D) is a carrier if:
od(v) = id(v) = 1

D₁:

Carrier in D₁ is vertex 2.

Definition 51:ISOLATED VERTEX
A vertex v in V(D) is an isolated vertex if:
od(v) = Id(v) = 0

D₁:

Isolated vertex in D₁ is vertex 1.

Definition 52:SUBDIGRAPH
A digraph H is called a subdigraph of a digraph D if V(H) is a subset of V(D) and A(H) is a subset of A(D).

D₁:

H₁:

Definition 53:SYMMETRIC
A digraph D is symmetric if whenever {(u,v)} C A(D), then {(v,u)} C A(D) as well.

D₁:

{(1,2)} С A(D₁)

{(2,1)} С A(D₁)

Definition 54:DIRECTED WALK
Let D be a digraph. A sequence w : u = u₀, u₁, .. u_k = v of vertices of D such that u is adjacent to u_i+1 for all i(1<i<k-1) is called a(directed) u-v walk of length k in D. The number of occurrences of arcs on a walk is the length of the walk.

D₁:

Walk : [1,2,3]

Length : 2

Definition 55:DIRECTED TRAILD AND DIRECTED PATH
A walk in which no arc is repeated is a (directed) trail; while a walk in which no vertex is repeated is a (directed) path.

D₁:

Trail : [1,2,1]

Path : [1,2]

Definition 56:UNDERLYING GRAPH
If a digraph D is an orientation of a graph G, then G is the underlying graph of D.

D₁:

G₁:

Digraph D₁ is an orientation of a graph G₁, there for G₁ is the underlying graph of D₁.

Definition 57:CONNECTED AND STRONG
A digraph D is connected (sometimes called weakly connected) if the underlying graph G is connected. A digraph D is strong (sometimes called strongly connected) if D contains both a u – v path of a v – u path for every pair, u,v of distinct vertices of D.

D₁:

G₁:

D₁ is connected because its underlying graph G₁ is connected.

D₁:

D₁ is strong because it contain a [1,2] path and [2,1] path.

Definition 58:DIRECTED DISTANCE
Let u,v Є V(D). The directed distance or more simply, the distance d(u,v) from u to v is the length of the shortest u – v path in D. A u – v d(u,v) path of length is a u-v geodesic.

D₁:

d(1,2) = 1

d(2,3) = 1

d(1,3) = 2

END.